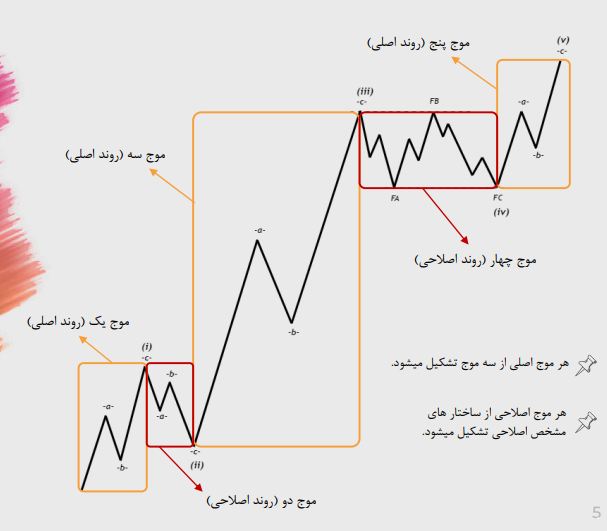
بررسی انواع ساختارها
1- ایمپالس (impulse)
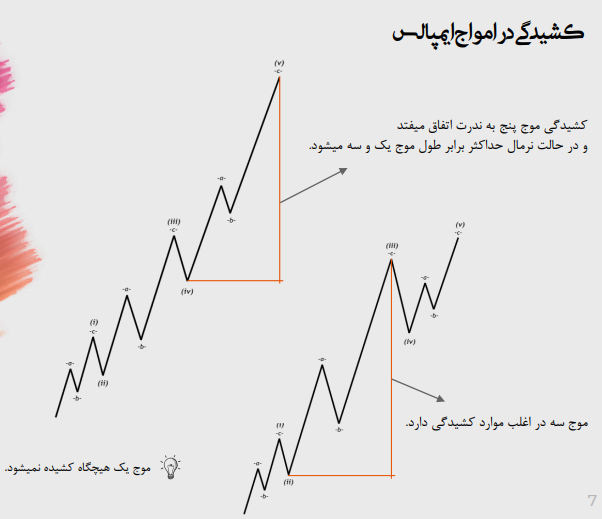
کشیدگی در امواج ایمپالس:
قوانین امواج ایمپالس:
قانون اول:
موج دو هیچگاه از ابتدای موج یک پایین تر کشیده نمیشود.
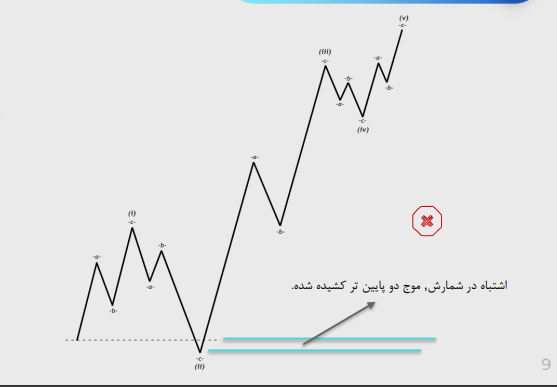
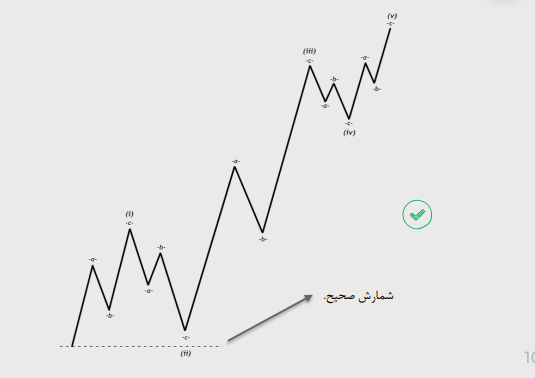
قانون دوم:
موج سه هیچگاه کوتاه ترین موج نیست.
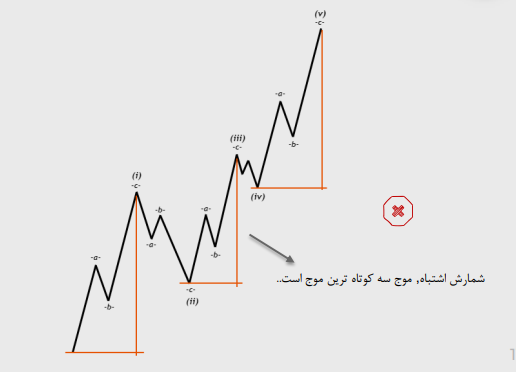
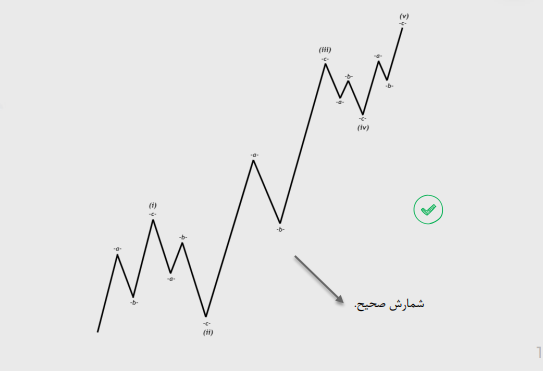
قانون سوم:
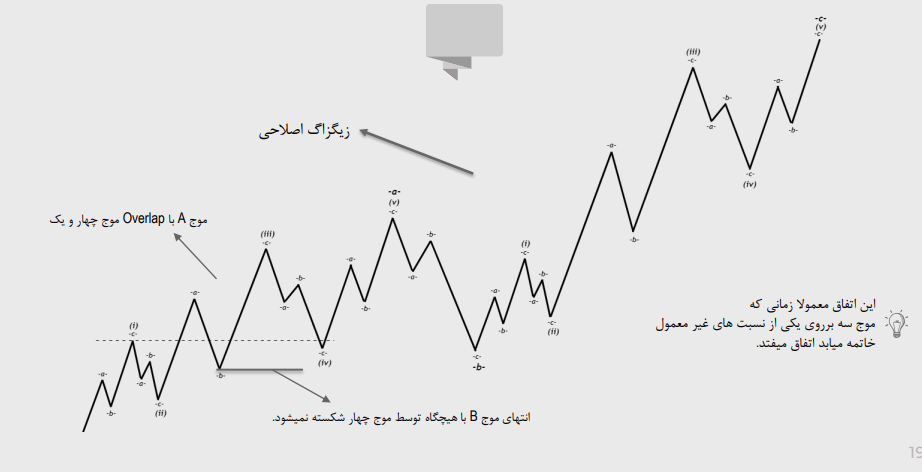
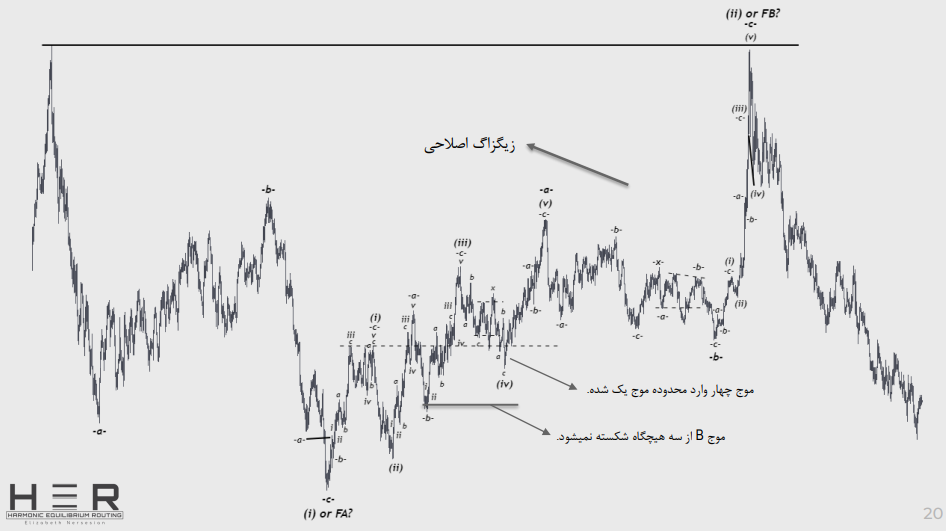
موج چهار هیچگاه وارد محدوده موج یک نمیشود.
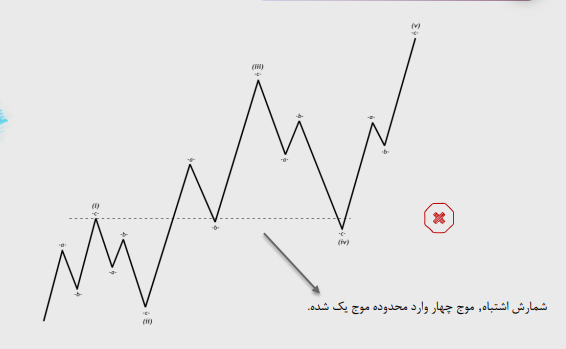
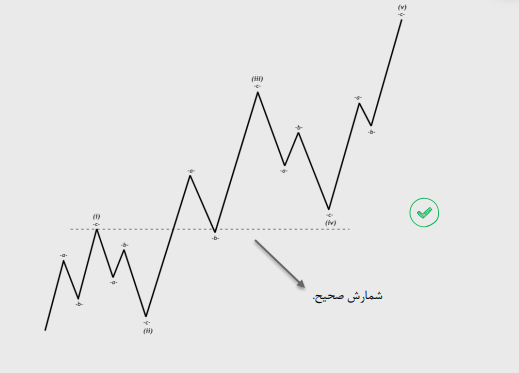
قانون چهارم:
موج چهار هیچگاه انتهای موج B از سه نمیشکند و اغلب نزدیک آن نمیشود.
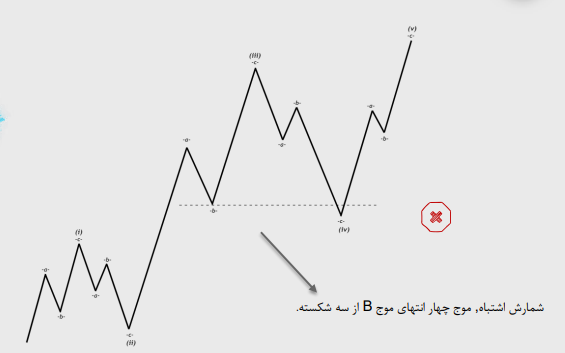
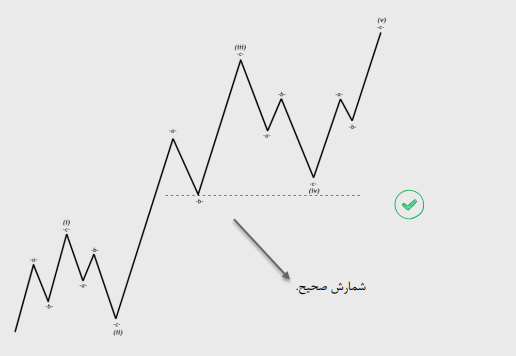
قوانین گفته شده در هیچ شرایطی نقض نمی شوند. اما در برخی مواردی که ذکر می شود قابل تغییر است.
شرایط خاص قانون شماره یک:
با توجه به ساختار قبل و ساختار جدید شکل گرفته کندل موج دو میتواند کمی انتهای موج یک بشکند. اما سریعا برگشت زده شده و کندل بالاتر از انتهای موج یک بسته می شود. اصولا این اتفاق در تایم فریم های پایین و به ندرت پیش می آید.
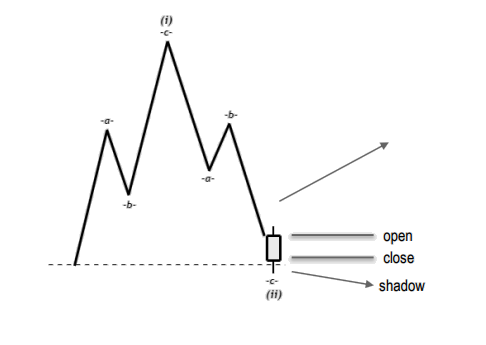
شرایط خاص قانون شماره سه:
موج چهار در امواج مثلث مورب (دیاگونال) . در الیوت کالسیک وارد محدوده موج یک میشوند. در الیوت هارمونیک امواج دیاگونال وجود ندارد اما موج چهار در شرایطی میتواند وارد محدوده موج یک شود. این اتفاق در امواج اصلاحی می افتد و یکی از امواج A یا C میتوانند مانند شکل روبه رو باشند. در الیوت هارمونیک امواج دیاگونال شروع کننده یا پایانی وجود ندارد. و در تمامی موارد امواج اصلی به صورت سه موج حرکت میکنند. در هیچ شرایطی موج B از سه شکسته نمیشود.
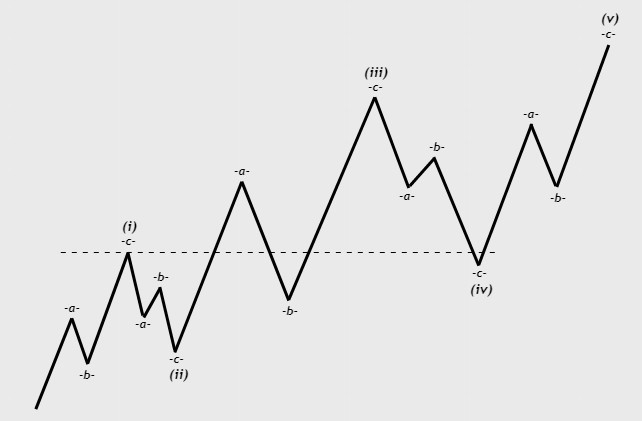
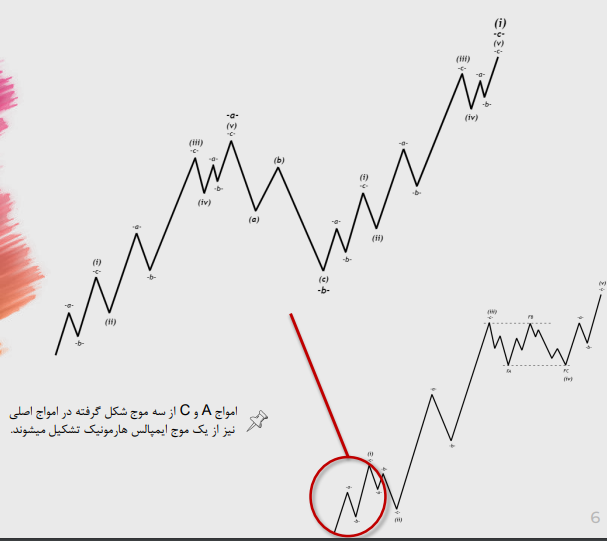
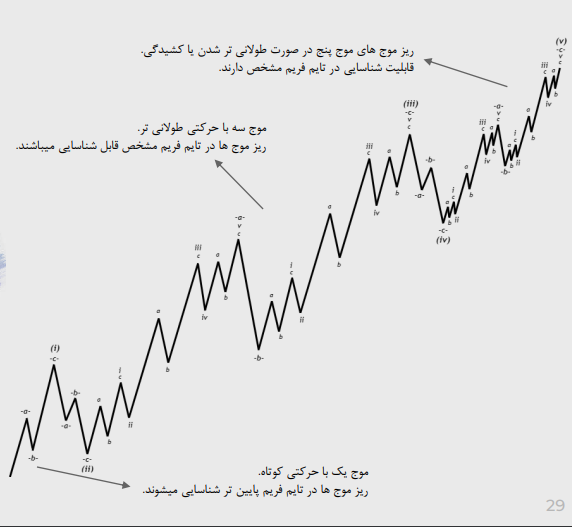
تناوب در ساختارهای ایمپالس
شماره 1:تناوب میان عمق امواج اصلاحی
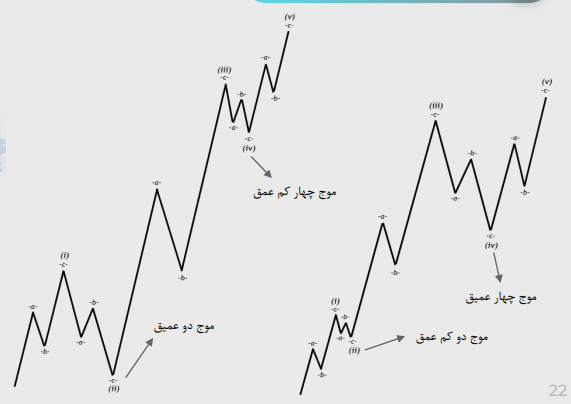
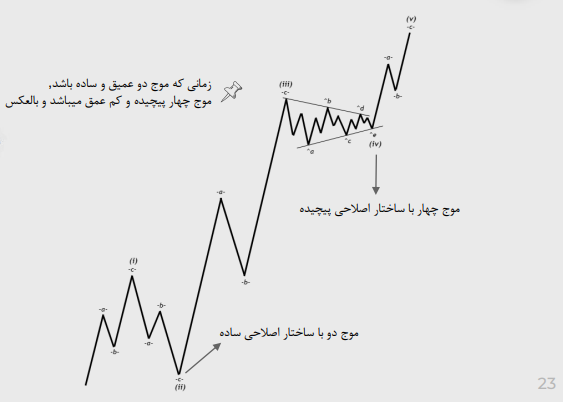
شماره 2: تناوب میان ساختار امواج اصلاحی
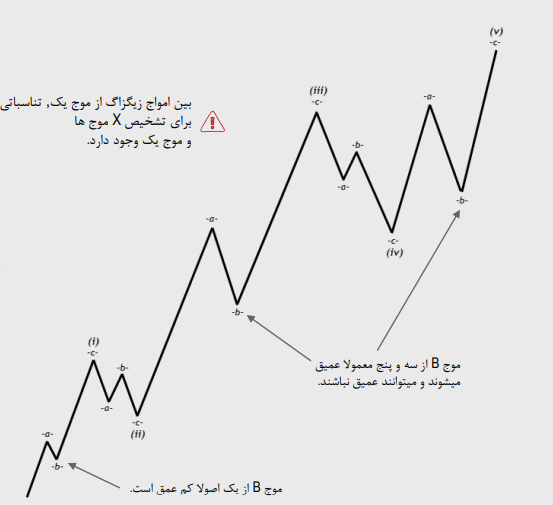
ساختار زیگزاگ از هر موج اصلی ایمپالس
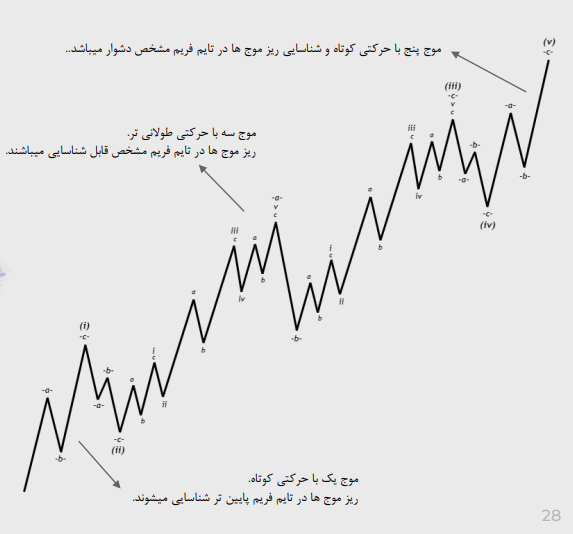
بررسی امواج و ریز موج ها
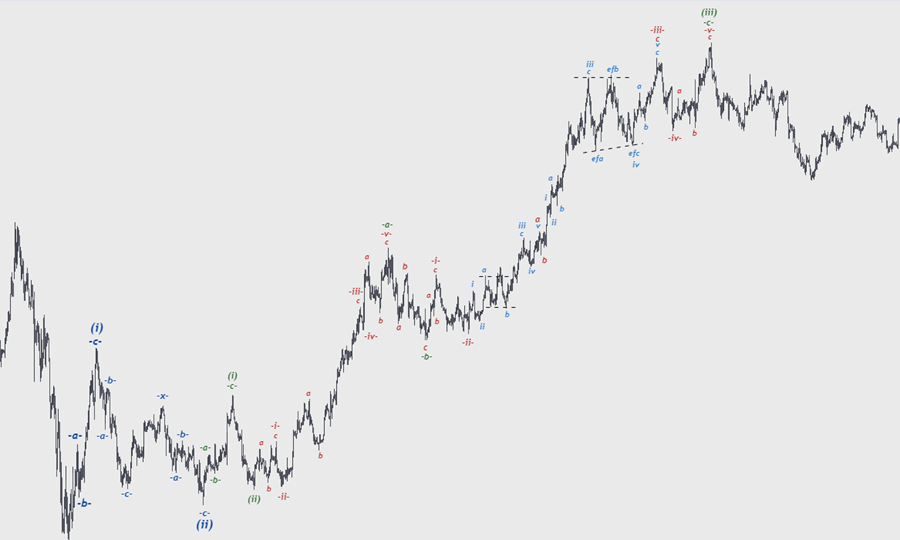
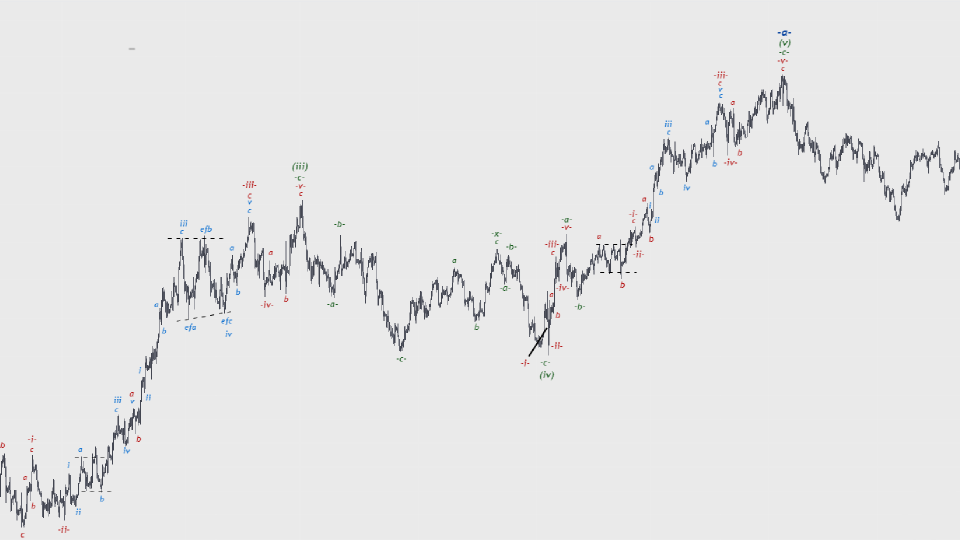
ساختارهای اصلاحی
ساختارهای اصلاحی ساده:
- (زیگزاگ ساده (ZigZag Simple)………………(c) (b) (a)
- دابل زیگزاگ(ZigZag Double)………………..(c) (b) (a)_(x)_(c) (b) (a)
- تریپل زیگزاگ (ZigZag Triple)……………….. (c) (b) (a)_(x)_(c) (b) (a)_(x)_(c) (b) (a)
ساختارهای اصلاحی پیچیده:
- فلت ها (اصلاح مسطح ساده) Flats
- اکسپندِد فلت ها(اصلاح مسطح بسط داده شده) Expanded Flats
- مثلث ها (Triangles)
نحوه لیبل گذای ساختار های اصلاحی:
اصلاح مسطح ساده: FA, FB, FC
اصلاح مسطح بسط داده شده:EFA,EFB,EFC
مثلث ها: A, ^B, ^C, ^D, ^E^ :
مثلث غیرعادی: EF^A, EF^B, EF^C, EF^D. EF^E
قوانین ساختارهای اصلاحی:
1- ساختار های اصلاحی تنها در امواج رو به رو توسعه میابند.موج (ii) – موج (iv) – موج (B ) – موج (X)
2- تمامی امواج اصلاحی میتوانند از هرکدام از ساختارهای اصلاحی تشکیل شوند. تنها موج دو هیچگاه از یک مثلث تشکیل نمی شود.
3- هر اصلاحی, ممکن است از ساختارهای اصلاحی از درجه پایین تر درون هر ساختاری از درجه بالاتر تشکیل شود.
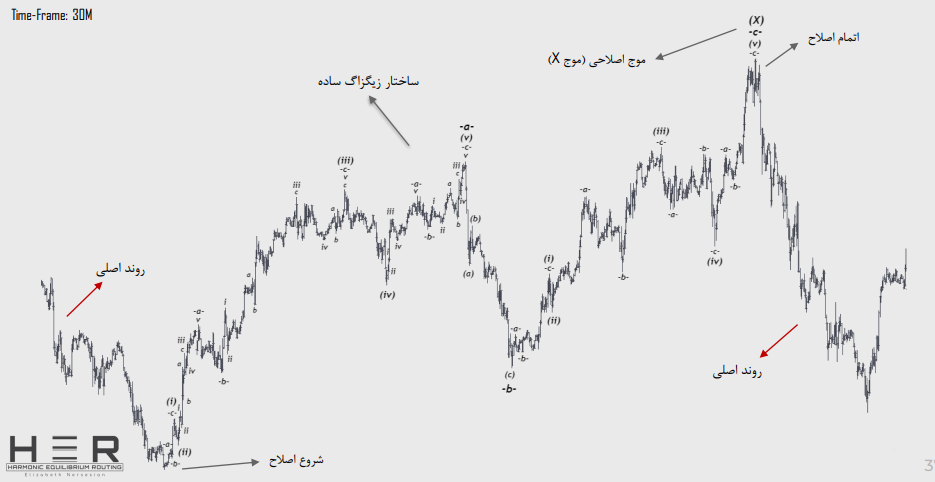
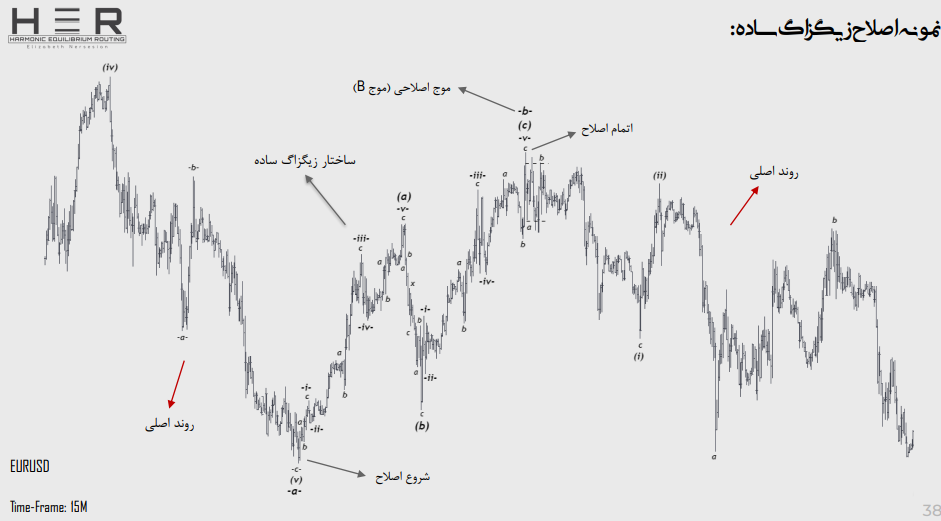
ساختارهای اصلاحی ساده:
اصلاح زیگزاگ ساده:
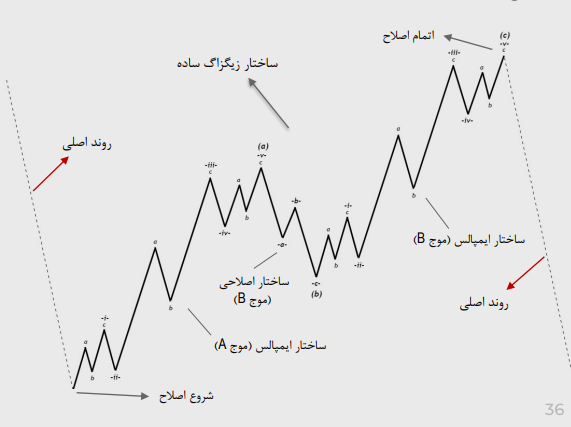
نمونه اصلاح زیگزاگ ساده:
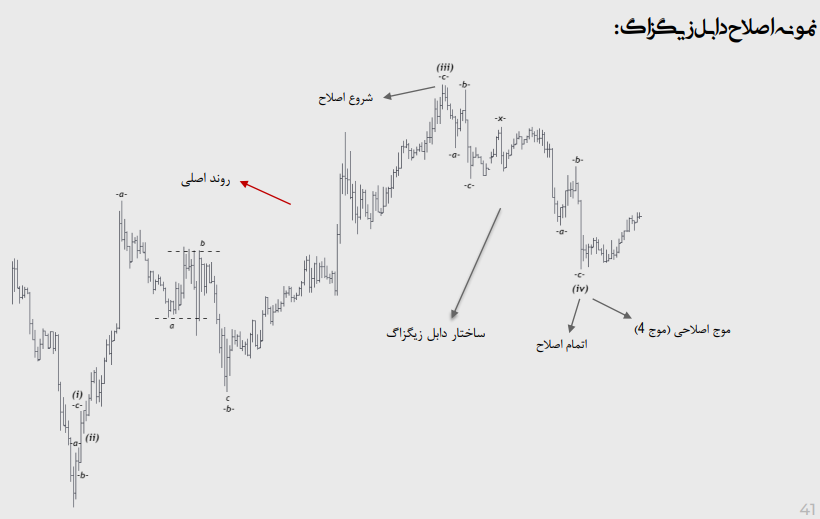
اصلاح دابل زیگزاگ:
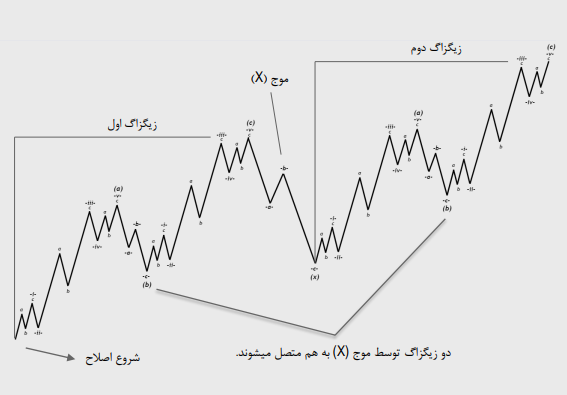
نمونه اصلاح دابل زیگزاگ :
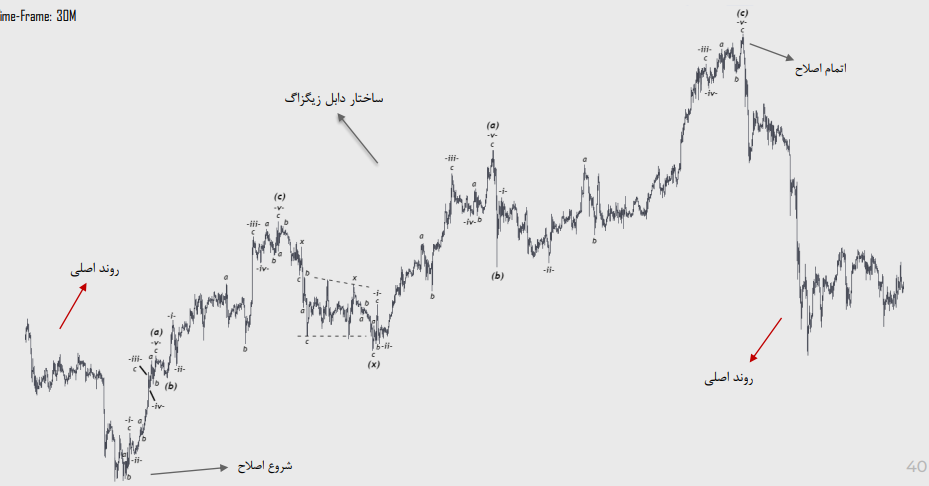
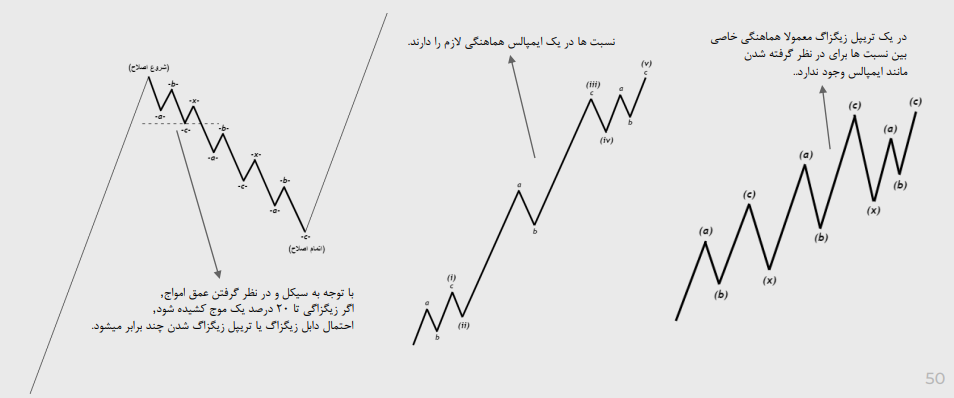
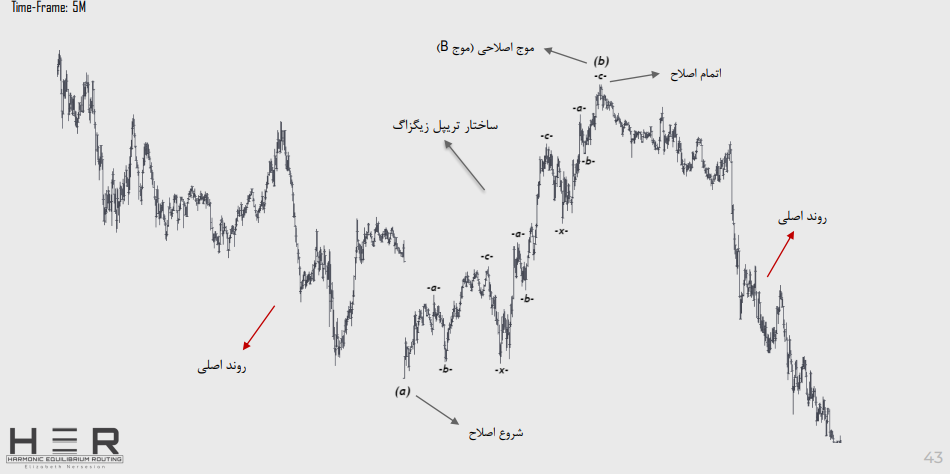
اصالح تریپل زیگزاگ:
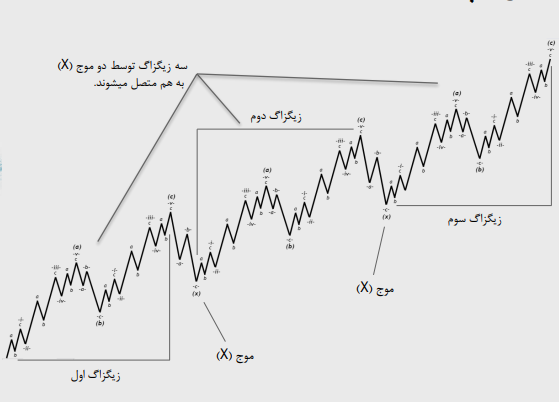
نمونه اصلاح تریپل زیگزاگ:
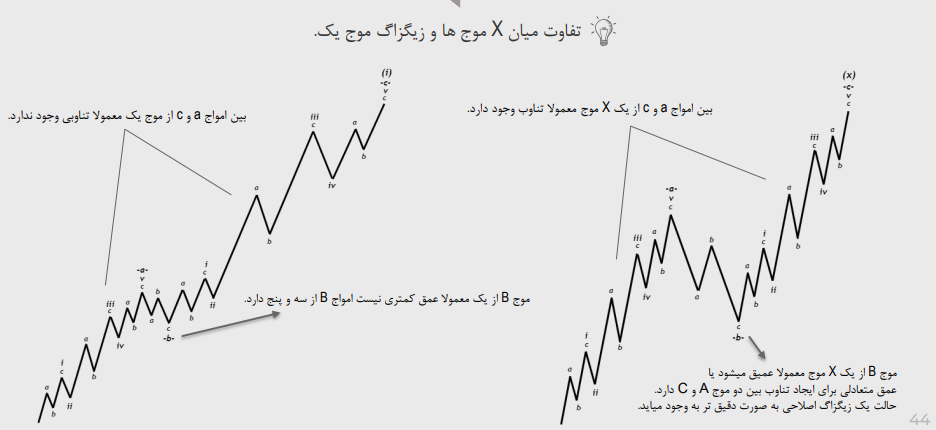
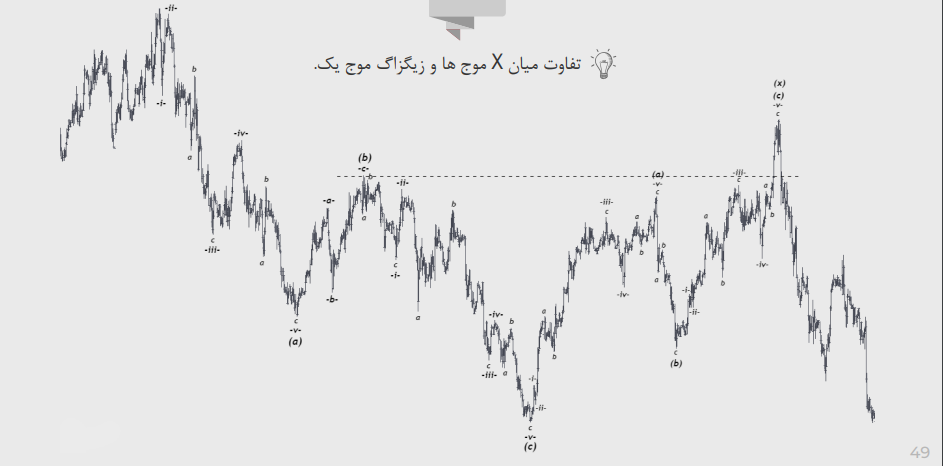
تفاوت میان X موج ها و زیگزاگ موج یک:
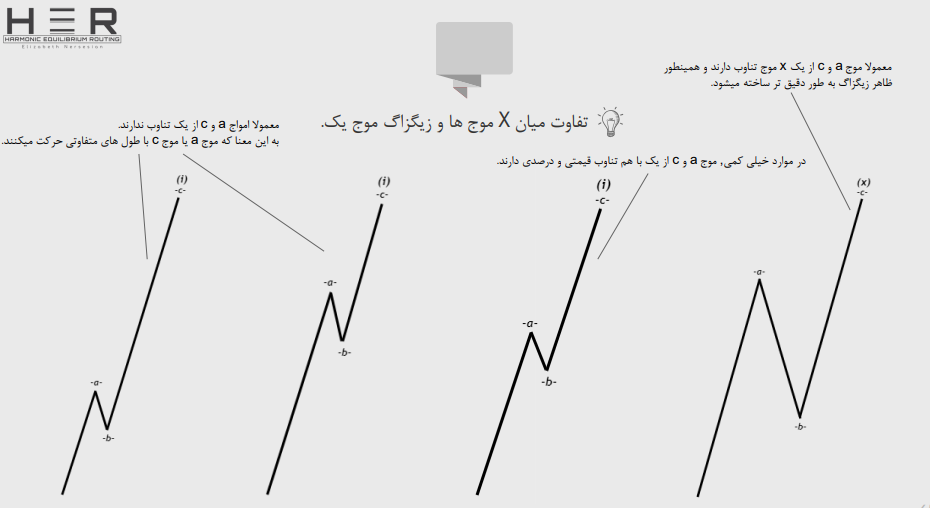
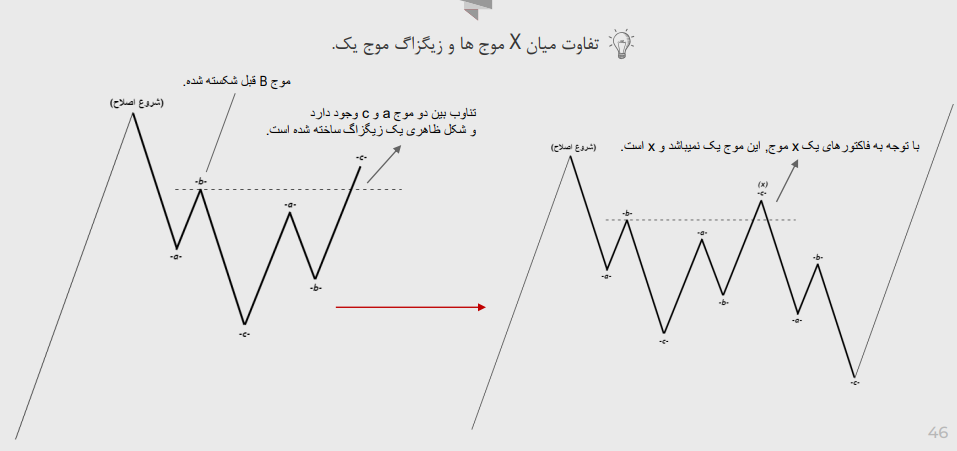
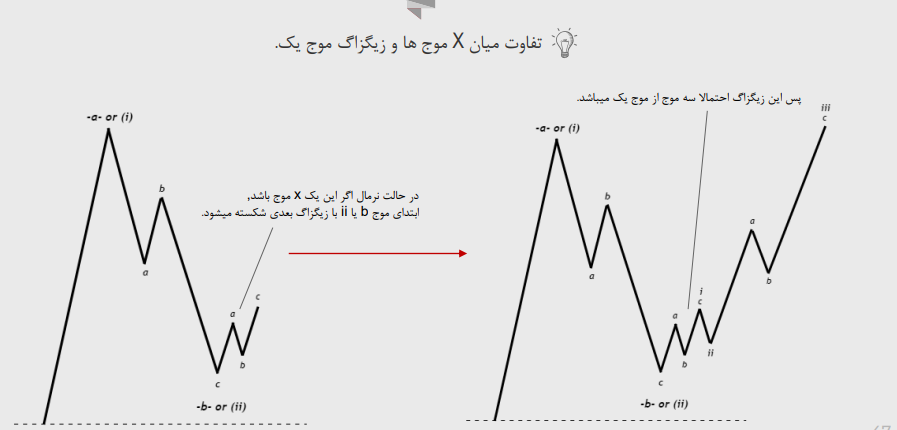
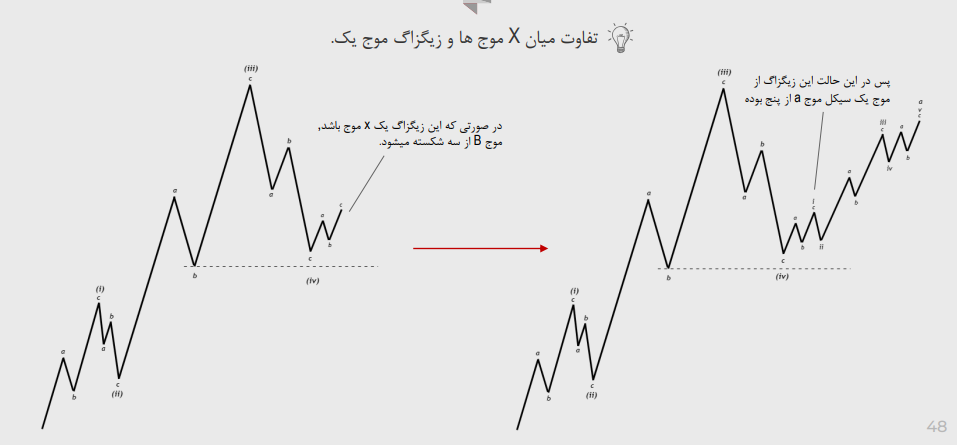
تشخیص تشکیل دابل زیگزاگ ها یا تریپل زیگزاگ ها و تفاوت میان یک ایمپالس و تریپل زیگزاگ: